Samenvatting voor wiskunde - Ruimtelijke figuren
Kubus
Een kubus is een vierkant blok waarvan alle zijden even lang zijn. Dus: de lengte, breedte en hoogte zijn gelijk. Een kubus heeft zes zijvlakken en elk zijvlak is een vierkant. Je zou dus kunnen zeggen: een kubus is een vierkant, maar dan in 3D. Een voorbeeld van een kubus is een dobbelsteen. Voor de inhoud van een kubus geldt de formule: inhoud = lengte x breedte x hoogte. Stel dat we een kubus hebben met zijden van lengte 5 cm, dan is de inhoud dus: 5 x 5 x 5 = 125 cm3.
Balk
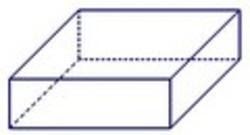
Een balk lijkt heel erg op een kubus. Het verschil is dat de zijvlakken uit rechthoeken bestaan in plaats van uit vierkanten. De inhoud van een balk kunnen we berekenen met dezelfde formule als de inhoud van een kubus, dus: inhoud = lengte x breedte x hoogte. Stel dat we een balk hebben met lengte 3 cm, breedte 4 cm en hoogte 5 cm. De inhoud is dan: 3 x 4 x 5 = 60 cm3.
Prisma
Een prisma is een 3D figuur waarbij alle vlakken (op twee na) een rechthoek zijn. De twee vlakken die geen rechthoek zijn, hebben een andere vorm. Wat die vorm precies is, dat verschilt per prisma. Het kan een driehoek zijn, dan krijg je dit figuur:
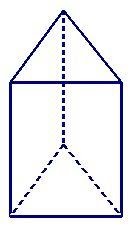
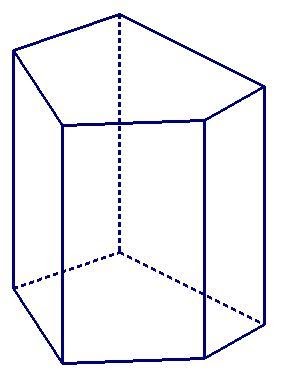
Vijfhoek prisma
Het kan ook een vijfhoek zijn, dan krijg je dit figuur:
En zo zijn er nog veel meer vormen mogelijk. Eén van de twee vlakken met een andere vorm noemen we het grondvlak. De inhoud van een prisma bereken je met de formule: inhoud = oppervlakte grondvlak x hoogte. De hoogte is de lijn die de twee grondvlakken met elkaar verbindt. Stel dat we een prisma hebben waarvan de oppervlakte van het grondvlak 12 cm2 is en de hoogte is 6 cm, dan is de inhoud dus: 12 x 6 = 72 cm3.
Piramide
Waarschijnlijk weet je wel hoe een piramide eruit ziet, maar wiskundig omschrijven we een piramide als volgt: een 3D figuur met een grondvlak en vier driehoekige zijvlakken. Hier zie je een voorbeeld van een piramide.
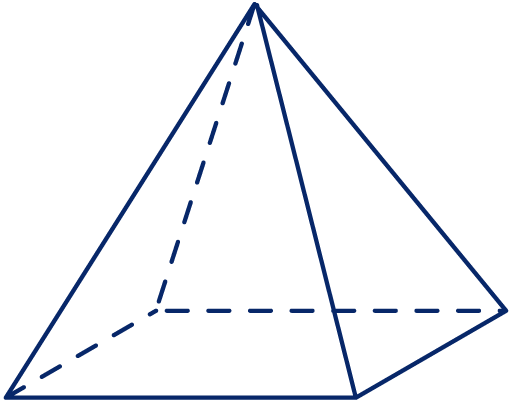
Je ziet dat het grondvlak hier een vierkant is en dat er vier zijvlakken zijn met een driehoekige vorm. Voor de inhoud van een piramide geldt: inhoud = 1/3 x oppervlakte grondvlak x hoogte. Stel dat we een piramide hebben waarvan de oppervlakte van het grondvlak 5 cm2 is en de hoogte is 3 cm, dan is de inhoud: 1/3 x 5 x 3 = 5 cm3.
Cilinder
Een cilinder is een ruimtelijk figuur dat de vorm heeft van een buis. Het grondvlak van een cilinder heeft de vorm van een cirkel. De inhoud van een cilinder bereken je met de formule: inhoud = oppervlakte grondvlak x hoogte. Aangezien het grondvlak een cirkel is, kunnen we voor de oppervlakte van het grondvlak de formule voor de oppervlakte van een cirkel gebruiken. Eerder hebben we geleerd dat die formule π keer r^2
2
is. De hoogte van een cilinder vind je door een rechte lijn te trekken van de ene cirkel naar de andere. In deze tekening zie je hoogte en de straal aangegeven in de cilinder.
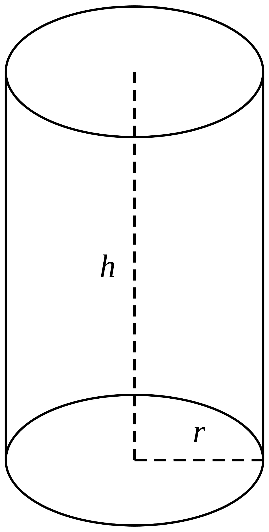
Stel dat de straal van de cirkel 3 cm is en de hoogte van de cilinder is 5 cm. Voor de inhoud van de cilinder berekenen we eerst de oppervlakte van het grondvlak. Dat is π x 32. Dat antwoord vermenigvuldigen we met de hoogte, dus met 5. Uiteindelijk vinden we dan een inhoud van ongeveer 141 cm3.
Kegel
Een kegel is een ruimtelijk figuur met een cirkel als grondvlak dat uitloopt in een punt. Eigenlijk lijkt een kegel heel erg op een piramide; het enige verschil is dat het grondvlak een cirkel is. Hier zie je een voorbeeld van een kegel.
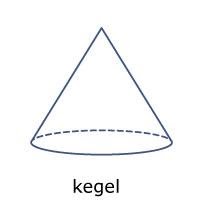
Voor de inhoud van een kegel geldt dezelfde formule als voor de inhoud van een piramide. Dus: 1/3 x oppervlakte grondvlak x hoogte. Aangezien het grondvlak hier een cirkel is, net als bij een cilinder, kunnen we voor de oppervlakte van het grondvlak de formule voor de oppervlakte van een cirkel gebruiken (π * r2).
Stel dat de cirkel een diameter heeft van 4 cm en de hoogte van de kegel is 6 cm. Voor de inhoud berekenen we dan eerst de oppervlakte van het grondvlak. Denk eraan dat je de diameter door de helft moet doen om de straal te krijgen. De straal is dus 2 cm. Voor de oppervlakte van het grondvlak doen we dan: π x 22 en het antwoord daarvan vermenigvuldigen we met de hoogte en dat is 6. We vinden dan een inhoud van ongeveer 75 cm3.
Bol
Een bol is een ruimtelijk figuur dat de vorm heeft van een balletje. Hier zie je een voorbeeld van een bol.

Voor de inhoud van een bol geldt de volgende formule: 4/3 x π x r3 . Hierbij geldt dat r de straal is van de bol, die vind je door een lijn te trekken vanaf het midden van de bol naar de rand. Eigenlijk is dat hetzelfde als bij een gewone cirkel. Stel dat de straal van de bol 5 cm is, dan is de inhoud: 4/3 x π x 53 = ongeveer 523 cm3.
Tot zover de samenvatting over ruimtelijke figuren. Vergeet niet om ook de andere uitlegvideo’s voor wiskunde te bekijken, zodat je straks goed voorbereid bent op het eindexamen!





