Samenvatting voor wiskunde - Rente
Vandaag gaan we kijken naar hoe rente werkt en hoe lang het bijvoorbeeld duurt voordat ons spaargeld verdubbeld is. En wat nou als iets juist steeds minder waard wordt? Hoe lang duurt het dan totdat de waarde gehalveerd is? Ook dat bespreken we in deze samenvatting.
Rekenen met rente
Als we met rente willen rekenen over een langere tijd, dan is er sprake van een exponentieel verband. Laten we heel even ons geheugen opfrissen door nog een keer te kijken naar de formule voor een exponentieel verband. Dat was namelijk:
N = b * gt
B is het begingetal, g de groeifactor en t is het aantal jaar dat voorbij is gegaan. Als we het over rente hebben, dan betekent dit dat b de hoeveelheid spaargeld is waarmee we beginnen. De groeifactor g kunnen we berekenen met het rentepercentage dat we krijgen. Ook weten we ondertussen natuurlijk al hoe we een groeifactor berekenen, namelijk met de formule: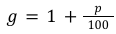 
. Waar g dus de groeifactor is en p het groeipercentage, of in dit geval, het rentepercentage. Als het goed is ken je deze twee formules al, maar het blijft een gedoe hè, al die formules!
Rente berekenen: voorbeeld
Stel je voor dat jij €7.000 op de bank hebt staan en dat zij een rentepercentage uitbetalen van 4% per jaar. Eerst moeten we dan de groeifactor berekenen. Dat doen we door het rentepercentage in te vullen in onze formule voor de groeifactor. Dan krijgen we: 
. Dus, we delen het percentage door 100 en tellen er 1 bij op. Dit komt uit op 1,04. Als we ons spaargeld een jaar op de bank zetten, krijgen we: N = 7.000 * 1,04. We doen namelijk ons spaargeld keer de groeifactor. Dit komt uit op €7.280. We hebben dus €280 verdiend in één jaar tijd. Maar, het mooie is dat als we het nu nog een jaar laten staan, dat we nu rente krijgen over meer geld!
Na twee jaar hebben we namelijk: 7.000 * 1,04 * 1,04 = 7571,2. En krijgen we dus €291,2 rente over het tweede jaar. Na drie jaar zouden we krijgen: 7.000 * 1,04 * 1,04 * 1,04=7874,05. We dus €302,85 rente over het derde jaar. Zo kunnen we voor eeuwig doorgaan. Maar, hoe komen we nou bij die exponentiële formule waar we het in het begin over hadden?
We kunnen 1,04 keer 1,04 keer 1,04 natuurlijk ook makkelijk schrijven als 1,04 tot de macht 3 (1,043 ). Als we dus opschrijven: g tot de macht t (gt), dan kunnen we voor t telkens het aantal jaar invullen over hoe lang we rente krijgen. Je krijgt dan dus weer de formule N = b * gt, waarbij N de hoeveelheid spaargeld is die we hebben aan het eind van het aantal jaar dat we rente krijgen, b de hoeveelheid spaargeld is waarmee we zijn begonnen, g de groeifactor is en t het aantal jaar is dat we rente krijgen. Als we dus willen weten hoeveel spaargeld we zouden hebben na 10 jaar, dan kunnen we dat makkelijk vinden door de formule in te vullen. We krijgen dan: N = 7000 * 1,0410. Als we dit invullen op onze rekenmachine krijgen we €10.361,71.
Wanneer is je spaargeld verdubbeld?
We vragen ons nu af wanneer het spaargeld dat we in het begin hadden is verdubbeld. Eigenlijk willen we dus weten na hoeveel jaar rente we b*2 hebben gedaan. Dit gedeelte van de formule, namelijk g tot de macht t, moet dus gelijk zijn aan 2, want dan krijgen we b*2. We schrijven dus op: gt =2. De groeifactor kunnen we invullen. Die is namelijk 1,04. Dus we krijgen 1,04t = 2. We moeten nu dus uitzoeken wat we voor t moeten invullen om boven de 2 te komen. Bij 2 zijn we namelijk verdubbeld, en we willen het aantal jaren t weten waarna we voor het eerst zijn verdubbeld.
We hebben net al een keer 10 ingevuld voor t en toen waren we nog lang niet verdubbeld, dus laten we beginnen met 15. We krijgen dan dus 1,04 tot de macht 15, en dat is gelijk aan 1,80. We moeten dus nog hoger zitten. Als we 1,04 tot de macht 17 doen, krijgen we 1,95. We zijn er dus bijna, maar nog niet verdubbeld! Als we nu 1,04 tot de macht 18 doen, dan krijgen we 2,03. We zijn dan dus voor het eerst boven de 2. Dit betekent dat de verdubbelingstijd 18 jaar is. Na 18 jaar hebben we ons spaargeld dus verdubbeld bij een rentepercentage van 4%.
Negatieve rente
Hartstikke mooi natuurlijk, dat verdubbelen, maar het kan natuurlijk ook voorkomen dat iets juist elk jaar minder waard wordt. Dit is het geval als de groeifactor minder is dan 1. Stel je bijvoorbeeld eens voor dat je een auto hebt gekocht. Elk jaar wordt die weer minder geld waard, omdat hij ouder wordt. We zeggen bijvoorbeeld dat jouw auto elk jaar 10% minder waard wordt. We kunnen dan weer dezelfde formule als net gebruiken om de groeifactor te berekenen. We krijgen dan: .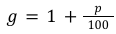
Dit keer vullen we voor p -10 in, aangezien het minder waard wordt en dus een negatief getal moet zijn. We krijgen dan 
. We doen dus -10 gedeeld door 100 + 1. Dit komt uit op 0,90. Onze groeifactor is dus 0,9. Stel nou dat jouw auto €8.000 waard was toen je ‘m kocht. Elk jaar vermenigvuldigen we de waarde van de auto met de groeifactor van 0,9. Na 1 jaar is de auto dus: €8.000 keer 0,9 is €7.200 waard. Bij elk extra jaar doen we telkens weer keer 0,9, dus de formule wordt nu: N=8000 * 0,9t . Hier kunnen we dus het aantal jaar invullen dat we de auto hebben en dan krijgen we de waarde die het tegen die tijd heeft.
Halveringstijd berekenen
Maar: wat als we nou de halveringstijd willen weten? Ofwel, na hoelang is de waarde van auto gehalveerd? Dit keer moet het eerste gedeelte van de formule dus 0,5 zijn. Want als we 8000 keer 0,5 doen, dan is het gehalveerd. We moeten dus oplossen: 0,9t =0,5.
We moeten nu uitzoeken wat we voor t moeten invullen om onder de 0,5 te komen. Bij 0,5 zijn we namelijk gehalveerd, en we willen het aantal jaren t weten waarna we voor het eerst zijn gehalveerd. Laten we beginnen met het invullen van 5. We krijgen dan dus 0,9 tot de macht 5, en dat is gelijk aan 0,59. We moeten dus nog hoger zitten voor de waarde van t. Als we 0,9 tot de 6de doen, dan krijgen we 0,53. We zijn er dus bijna, maar nog niet gehalveerd! Als we nu 0,9 tot de macht 7 doen, dan krijgen we 0,48. We zijn dan dus voor het eerst onder de 0,5. Dit betekent dat de halveringstijd 7 jaar is. Na 7 jaar is de waarde van de auto voor het eerst gehalveerd.
